Premio Nobel de física 2024. Una alianza con la computación

Pablo H. Ibargüengoytia

El Dr. Pablo Ibargüengoytia es ingeniero en electrónica por la Universidad Autónoma Metropolitana. Maestro en Ciencias con especialidad en sistemas digitales por la Universidad de Minnesota, E.U.A. Doctorado en Ciencias de la Computación por la Universidad de Salford, Gran Bretaña, con especialidad en Inteligencia Artificial. Ingresó al Instituto de Investigaciones Eléctricas (IIE) en 1983, ahora Instituto Nacional de Electricidad y Energías Limpias. Se jubiló del instituto en agosto de 2019 y desde entonces fundó la compañía de base tecnológica Naatik A.I. Solutions para el desarrollo de aplicaciones de inteligencia artificial en las empresas e industrias del país. Es miembro de la Academia de Ciencias de Morelos.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

El día 8 de octubre se publicó a los ganadores del premio Nobel en Física 2024. Se trata de John J. Hopfield y Geoffrey E. Hinton por sus aportaciones en el aprendizaje automático de redes neuronales artificiales (RNA). Esta es un área de trabajo típica de los colegas en ciencias de la computación, más que de la física. ¿Les recuerda este caso a lo sucedido en 2016, con el premio Nobel de Literatura concedido a Bob Dylan? ¿Por qué se les otorga a estos investigadores? ¿En qué consisten sus logros? Demos un poco de antecedentes para comprender mejor su importancia.

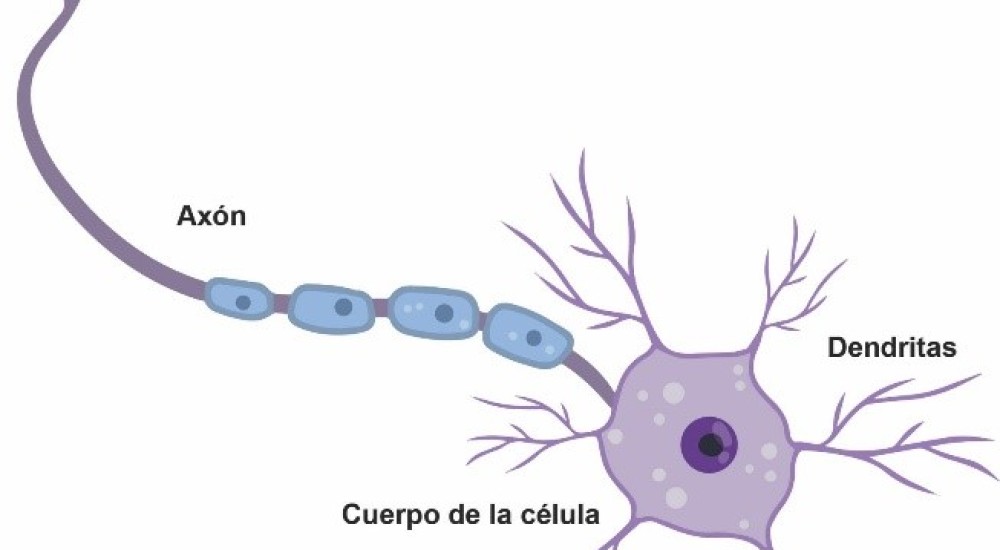
Las redes neuronales toman su nombre por la similitud con las neuronas del cerebro humano. Las neuronas son células nerviosas que procesan información. Están compuestas por el cuerpo de la neurona y dos tipos de ramales que salen de la neurona, el axón y las dendritas (Figura 1). Una neurona recibe señales provenientes de otras neuronas a través de las dendritas y transmite una señal procesada en el núcleo de la célula mediante el axón. Con estas interconexiones entre neuronas se generan gigantescas redes de neuronas que intercambian señales (información). La actividad de estas redes neuronales naturales permite realizar las actividades del cerebro, incluyendo el aprendizaje y la memoria.

La corteza cerebral humana está formada por un enorme número de neuronas (del orden de 10¹¹ neuronas, o cien mil millones). Estas ocupan una   superficie de 2,200 cm². Cada neurona puede establecer conexiones con tanto como mil (10³) o diez mil (10⁴) neuronas. En total, el cerebro humano contiene un número elevadísimo de interconexiones neuronales, representando aproximadamente 10¹⁴ a 10¹⁴ (de cien a mil billones).

Las redes neuronales artificiales (RNA) son estructuradas por expertos en ciencias de la computación tomando como inspiración el cómo se arman las redes neuronales naturales. La idea de las RNA es formar redes interconectadas del equivalente en computación de “neuronas”, que permitan el procesamiento de información y la clasificación de objetos.

Figura 1. Estructura básica de una neurona humana. Fuente: Banco de imágenes 123rf.

La Figura 2 muestra una “neurona” artificial básica, conocida también como perceptrón. La “neurona” puede tener varias entradas-que pueden recibir diferentes valores- y una salida, cuyo valor es el producto del procesamiento de información en la “neurona”. Las diferentes entradas tienen asignadas un parámetro w que puede tomar diferentes valores. Este parámetro es de suma importancia, ya que es el que se ajusta en el momento del entrenamiento de la red neuronal. Como se puede apreciar en la figura 2, la neurona realiza la suma ponderada de las entradas por sus parámetros w. Entonces, el primer paso en el    procesamiento de la neurona es 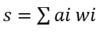 . Después el valor s se proyecta en una función llamada de activación. Es decir, se aplica la función con el valor s y se obtiene el valor final de salida de la neurona. Ese valor de salida puede ser la entrada a neuronas de las capas siguientes de la red.
 

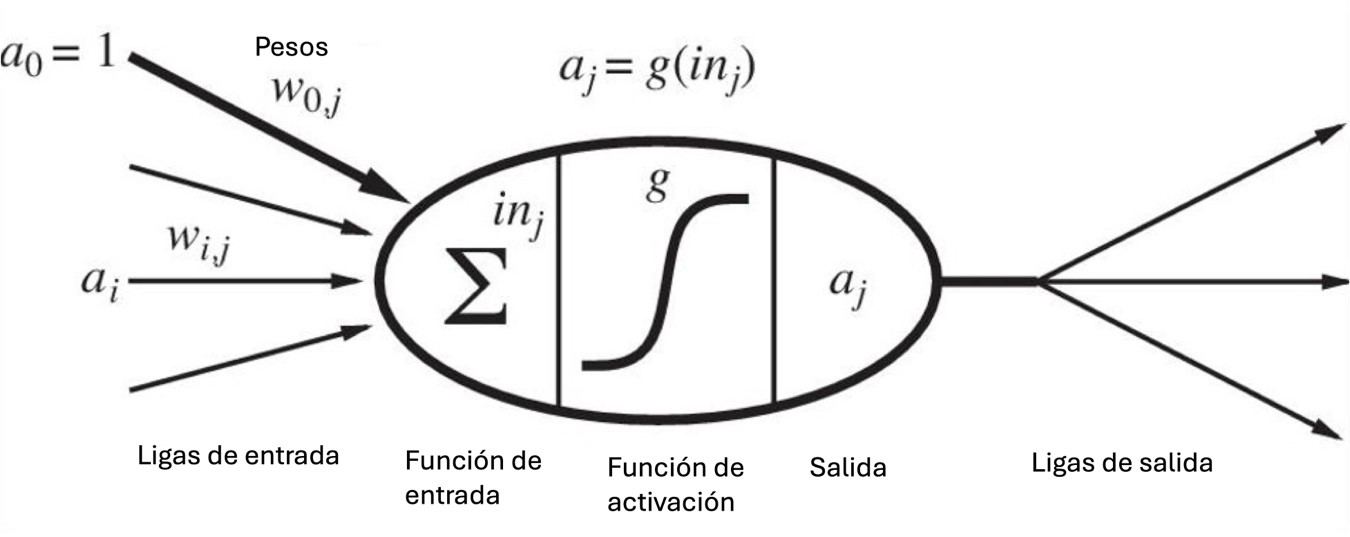
Figura 2. Neurona artificial básica. Fuente: S. Russell y Peter Norvig, Artificial Intelligence. A Modern Approach, Third Edition, Prentice Hall, 2010

La figura 3 muestra una RNA multicapa de tres entradas y dos salidas. Se puede utilizar en problemas cuya base de datos tenga tres columnas para los datos de entrada y dos columnas para los datos de salida.

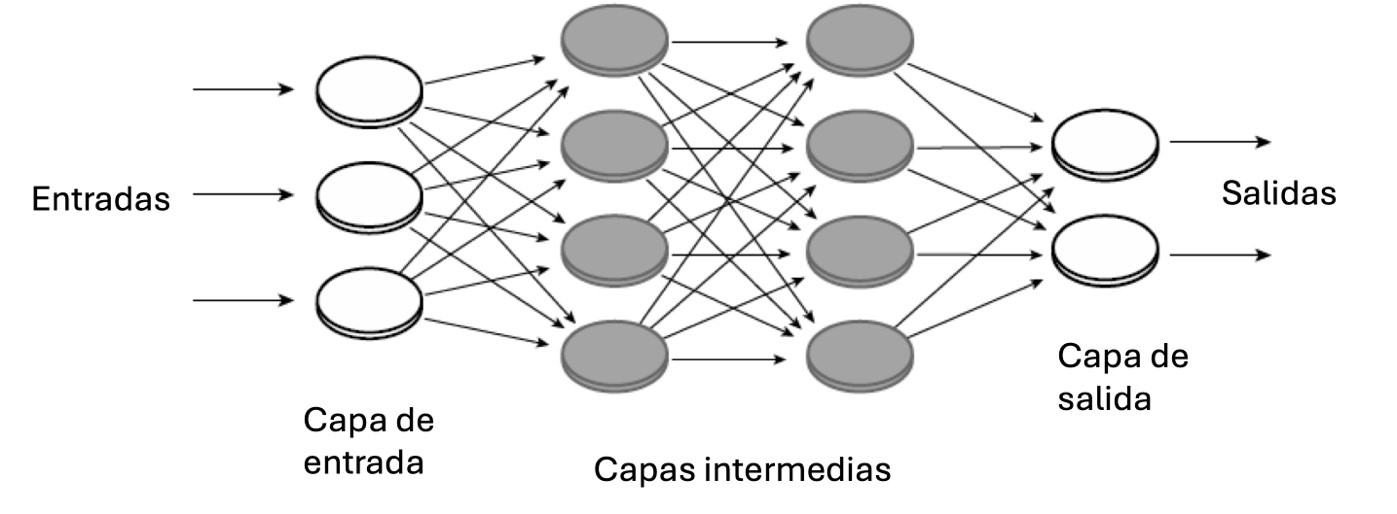
Figura 3. RNA multicapa de tres entradas y dos salidas. Fuente: Scientific Background to the Nobel Prize in Physics 2024, The Royal Swedish Academy of Sciences, 8 October 2024.

Una de las funciones básicas de las RNA es la clasificación de objetos. Para hacer esa función se requiere hacer un proceso de aprendizaje de la clasificación. Eso normalmente se conoce como entrenamiento de la red. Por ejemplo, en un negocio de servicios como telefonía celular, puede usarse una RNA para reconocer diferentes tipos de clientes. Las variables pueden ser: 1) la antigüedad del cliente, 2) el promedio de gasto mensual, 3) edad del cliente y 4) servicios que contrata. Estas cuatro son las variables y se utilizará una red con cuatro neuronas de entrada. Deberá traducir el valor de cada entrada a valor numérico. Por ejemplo, a la antigüedad de cliente se asigna el valor de: 1 para los antiguos; 2 para los de antigüedad media y 3 a los clientes nuevos. La respuesta de cada ejemplo es si el cliente es bueno, regular o malo y también se le asigna un valor de 1, 2 o 3. Si es bueno, sabremos que permanecerá con el servicio. Si es un cliente regular, se requiere consentirlo con alguna promoción. Y si el cliente es malo, se podría solicitar una entrevista personal. En este caso, la RNA tendrá 3 neuronas de salida. Entonces, para entrenar a la RNA en el proceso de clasificación de clientes, debemos presentarle ejemplos de clientes anteriores con sus cuatro características y la clasificación que se realizó por personal de la empresa. Los datos de entrenamiento será una tabla de 5 columnas, 4 para los parámetros del cliente y la última columna para el tipo de cliente. El número de filas en la tabla de entrenamiento serán los ejemplos de clientes que podamos recopilar. Si se recopilan ejemplos de clientes durante muchos años, podremos hacer que la RNA realice ese procedimiento de clasificación automáticamente.

El proceso de entrenamiento consiste en aplicar los valores a la entrada de la red y ajustar todos los parámetros w de las entradas a cada neurona de manera que se obtenga el valor esperado de salida. Se presenta el primer ejemplo con los 4 parámetros de entrada y el valor de salida: “tipo de cliente”. El valor de los parámetros se multiplica por el valor de w de cada entrada de neurona y se adquiere el valor de salida de cada neurona. Se propaga el valor en toda la red y se van modificando todos los parámetros w de tal manera que el valor resultante en la red corresponda al valor conocido de la salida. El proceso de ajuste de pesos w con todos los ejemplos de la tabla de entrenamiento forma un modelo que se utilizará en los próximos clientes para descubrir desde el inicio su tipo.

Aspectos a considerar para las RNA

Existen muchas formas de crear los sistemas de RNA y muchas formas de entrenarlas. Entre las diferentes formas de crear la red están:

• La selección de la función de activación. Es aquella función que se aplica a la suma ponderada de las entradas a la neurona. Existen funciones como escalón, parcialmente lineal, sigmoide o gaussiana.
• Estructura de la red. Puede ser de conexiones en una sola dirección (feed forward) o retroalimentadas con conexiones hacia neuronas anteriores.

Entre las formas de entrenamiento de RNA se tienen:

• Aprendizaje supervisado. Para este entrenamiento se utiliza un conjunto de datos donde se proporciona la respuesta o salida correcta de cada patrón de datos de entrada. El algoritmo ajusta el valor de los pesos w con cada ejemplo en los datos y se siguen ajustando con todos los patrones del entrenamiento.
• Aprendizaje no supervisado. Se utiliza un conjunto de datos sin especificar la salida. El algoritmo encuentra una correlación entre los ejemplos de los datos de entrada y organiza patrones en categorías a partir de las correlaciones descubiertas en los datos. En este caso se ajustan también los pesos w para conservar la categorización.
• Híbrido. Se refiere a una combinación de los métodos anteriores. Unos pesos w son calculados con algoritmos no supervisados y los demás con algoritmos supervisados.

Por supuesto existen diferentes algoritmos para ejecutar el entrenamiento y éstos son evaluados conforme a la exactitud de los resultados obtenidos, el tamaño y arquitectura de neuronas que es capaz de entrenar y la complejidad computacional al ejecutar el entrenamiento.

Aplicaciones de las RNA

Las redes pueden entrenarse con datos tales como imágenes, sonidos, tablas de valores entre otros, obteniéndose así aplicaciones comunes de RNA para resolver problemas o tomar decisiones. Entre las aplicaciones se encuentra:

• Reconocimiento de patrones. Una aplicación médica empleando RNA e información de radiografías de los pulmones de diferentes pacientes, podría permitir identificar a personas sanas o pacientes con Covid. Otro ejemplo, en este caso de la industria, sería el reconocimiento de un producto terminado correctamente en una línea de producción, contra un producto defectuoso.

• Categorización o agrupación. Dados ciertos datos de objetos con ciertos atributos, se pueden agrupar con características similares, formando grupos. Por ejemplo, categorización de clientes.
• Aproximación de funciones. Dados ciertos puntos medidos en una aplicación, se puede deducir la función que representan esos números comparándolos con valores de una función conocida.
• Pronóstico. Dados ciertos valores numéricos en el tiempo, se puede inferir el o los siguientes valores en el tiempo.
• Optimización. Seleccionar de entre un conjunto de soluciones a un problema, la más adecuada en cierta situación. Puede ser la solución más corta, más barata o más sencilla.
• Recuperación de contenido. Dadas imágenes en presencia de nubes, se puede deducir el contenido de la imagen en la ausencia de nubes.

Control. deducir el valor apropiado de una variable durante un proceso en base a los valores de las variables relacionadas. Por ejemplo en el control de velocidad de un vehículo.

Importancia de las contribuciones de los premiados

Ahora bien, la pregunta es ¿cuál es la relación entre lo que se acaba de exponer y los trabajos de dos científicos que ganaron el premio Nobel de física? (Fig. 4)

Figura 4. Ganadores del Premio Nobel de Física 2024. Fuente: Reuters (https://www.reuters.com/science/hopfield-hinton-win-2024-nobel-prize-physics-2024-10-08/)

El trabajo de John J. Hopfield comenzó en los años 80s, cuando estudiaba las ecuaciones de estado de un conjunto de átomos con momento magnético, dando lugar a un ferro-magneto a escala macroscópica. Un ferro-magneto es un metal que reacciona en presencia de campos magnéticos, como el hierro, el cobalto y el níquel. Hopfield sugirió que cada átomo representa un vértice de una red y las aristas con sus respectivos pesos representan la organización de momentos magnéticos y los estados estacionarios, es decir, los estados de energía mínima corresponden a soluciones óptimas para problemas representados por la red formada. Hopfield propuso una ecuación que asigna la energía a una red y resultó notablemente similar a la ecuación de entrenamiento de una red neuronal que en aquella época se comenzaban a estudiar. Hopfield propuso que las ecuaciones de entrenamiento de RNA pudieran ser usadas para describir materiales magnéticos. Adicionalmente, Hopfield mejoró su red proponiendo que se trabajara con nodos con valores analógicos en vez de valores binarios. Este modelo constituyó un ejemplo pionero en el uso de sistemas dinámicos para buscar soluciones de problemas difíciles de optimización discreta.

Cuando Hopfield utilizó su red, entrenada para minimizar la energía en otras aplicaciones como el procesamiento de imágenes, encontró que al presentarle a la red una imagen incompleta o distorsionada de algún objeto, la red restauraba el objeto a su forma original. Se consideró entonces que Hopfield realizó una contribución fundamental para el entendimiento de las potencialidades computacionales de las redes neuronales.

Por su parte, de 1983 a 1985, Geoffrey E. Hinton desarrolló una extensión estocástica del modelo de Hopfield, pero donde cada estado de la red se asigna con un valor de probabilidad dado por la distribución Boltzmann. Su modelo fue llamado la Máquina Boltzmann. Hinton desarrolló un algoritmo eficiente para el entrenamiento de las redes multicapa.

Una de las contribuciones importantes de Hinton, fue la demostración de la función de las capas intermedias de una RNA, que permitió realizar tareas que se consideraban insolubles cuando no se utilizaban capas intermedias.

La aportación de Hinton sobre los algoritmos de entrenamiento de redes neuronales de múltiples capas, dio paso a lo que ahora se conoce como aprendizaje profundo (Deep learning en inglés). Se refiere a redes formadas con enormes cantidades de capas intermedias, muy interconectadas. Redes como estas, previo al trabajo de Hinton, habían sido inviables debido a la dificultad computacional de entrenarlas. La aportación de Hinton hizo este entrenamiento factible.

Los resultados logrados con sistemas de aprendizaje profundo han sorprendido al mundo en el último par de años. Son las herramientas básicas de la nueva Inteligencia Artificial Generativa, como los paquetes ChatGPT, Copilot o Geminy.

El galardonar a estos dos científicos con el premio Nobel, significa un reconocimiento de cómo la física ha sido impulsora de avances y desarrollos de las RNA. Así mismo, las RNA han sido una herramienta muy poderosa de modelado y análisis en muchas áreas de la física. Ejemplos de ello son el desarrollo de nuevos materiales fotovoltaicos o la resolución de modelos climáticos basados en física. En los años 90s las redes neuronales profundas se usaron con éxito en el análisis de datos que condujeron al descubrimiento del bosón Higgs en el CERN.

Lo interesante de este premio Nobel es que científicos trabajando en sus campos de la física, encontraron formas de mejorar las capacidades de las redes neuronales artificiales y a su vez, las redes neuronales apoyaron fuertemente el trabajo y el adelanto de sus respectivos campos. Felicidades a los premiados y enhorabuena a todos los que usamos y seguiremos usando redes neuronales.

Referencias

Anil K. Jain, Jianchang Mao, K.M. Mohiuddin, Artificial Neural Networks: A Tutorial, IEEE Computer, Vol. 18, Num. 3, Marzo 1996

S. Russell y P. Norvig, Inteligencia Artificial: Un enfoque moderno, Prentice Hall, 2004

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos.