Tiranía de la mayoría

W. Luis Mochán

El Dr. W. Luis Mochán Backal es investigador titular del Instituto de Ciencias Físicas de la Universidad Nacional Autónoma de México y miembro de la Academia de Ciencias de Morelos

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

Un pequeño país

Había una vez un país llamado Mayoritlán. Era un país muy pequeño, conformado por apenas 51 pueblos. Sin embargo, tenía una fuerte cultura democrática. Cada tres años los ciudadanos de Mayoritlán realizaban una votación para elegir a sus 51 diputados, uno por cada pueblo, quienes representarían a sus habitantes para proponer nuevas leyes y cambios en las viejas leyes, argumentar sobre sus virtudes, discutir con los diputados rivales, insultarlos, pelear y finalmente, ante ciertas señales convenidas, levantar la mano para aprobar los cambios legislativos que encarnarían la transformación del país, una de tantas. Desde su fundación, en Mayoritlán sólo ha habido dos partidos políticos, el Partido Azul y el Partido Rojo. Curiosamente, los azules siempre han sido los preferidos por aproximadamente el 60% de los ciudadanos, mientras que los rojos han sido el partido favorito del 40% restante. En cierta elección hubo exactamente 51 ciudadanos en cada uno de los 51 pueblos y una investigación profunda ha permitido averiguar, a pesar de su secrecía, la forma en que votó cada uno de sus pocos ciudadanos, la cual se ilustra en la figura 1.

Figura 1: Preferencia electoral de cada ciudadano de cada pueblo de Mayoritlán. Los cincuenta y un pueblos y sus cincuenta y un ciudadanos están numerados del 1 al 51. Se señalan dos resultados particulares mediante cruces.

En lugar de nombrar los 51 pueblos, en la figura se han numerado del 1 al 51. Similarmente, en lugar de nombrar a los 51 ciudadanos, para proteger su privacidad y respetar el secreto del voto han sido numerados del 1 al 51. Así, el cuadrito azul en la columna 10 del renglón 20 de la figura (donde está centrada la cruz blanca) significa que el ciudadano 20 del pueblo 10 votó por el candidato del Partido Azul, mientras que el cuadrito rojo en el renglón 30 de la columna 40 (cruz gris claro) indica que el ciudadano 30 del pueblo 40 votó por el Partido Rojo. Contando pacientemente los cuadritos azules y rojos, notamos que hubo 1593 votos a favor de los azules y 1018 votos por los rojos de un total de 51×51=2601 votos, por lo cual los azules tuvieron la preferencia del 1593/2601=61% de la población y los rojos la del 1018/2601=39% restante, cercanos al 60% y 40% históricos mencionados arriba.

El resultado justo

Detengámonos un minuto y piense Ud., querido lector, ¿qué porcentaje de los cincuenta y un diputados considera Ud. que deberían corresponder al Partido Azul y qué porcentaje al Partido Rojo? ¿Creé Ud. que algo cercano a 30 azules y 20 rojos sería lo justo? Así, el porcentaje de azules y rojos en la Cámara Legislativa sería un fiel reflejo del porcentaje de pro-azules y pro-rojos en la ciudadanía, ¿no lo considera Ud. así?

Antes de mostrarle el resultado de la elección que estamos analizando, permítame volver a presentarle las preferencias de los ciudadanos, pero dejando caer los cuadros rojos para que se apilen en la parte baja de la figura y dejando flotar los cuadros azules para que se apilen arriba, renumerando a los ciudadanos de cada pueblo, como muestra la figura 2.

Figura 2: Preferencias electorales como en la figura 1 pero renumerando a los ciudadanos de cada pueblo para poner primero a los votantes del partido rojo y después a los del azul.

La figura recuerda a la silueta de una ciudad con grandes edificios de alturas diversas. Una forma de leerla es como un histograma, una gráfica que nos dice cuántos votos tendría cada partido en cada pueblo. Así, las primeras columnas nos dicen que los rojos obtuvieron 24 votos en el pueblo 1 y 21 votos en el pueblo 2, la séptima columna indica que sólo obtuvieron 13 votos en el pueblo 7 pero la columna 37 muestra que en el pueblo correspondiente tuvieron 27 votos. Si estudiamos las columnas blancas de arriba a abajo veremos que en el pueblo 1 los azules obtuvieron 51-24= 27 votos en el pueblo 1, 30 en el pueblo 2, etc.

La paliza

La figura 2 muestra además una línea horizontal que indica un umbral de 25 votos. Para ganar la elección en un pueblo con 51 ciudadanos, el candidato a diputado correspondiente debería sacar más de 25 votos, es decir, debe obtener 26 o más votos para tener mayoría. Como se ve en la gráfica, sólo en tres pueblos, el 38, 40 y 43 ganaron los rojos. Por lo tanto, sólo hubo tres diputados del Partido Rojo electos. Tres de cincuenta y uno son apenas el 5.9%. A pesar de haber tenido casi el 40% de la preferencia electoral, ganaron menos del 6% de los escaños. Por otro lado, los diputados del Partido Azul, a pesar de sólo tener alrededor del 60% de las preferencias, obtuvieron el 94.1% de los escaños.

En realidad, he de confesar que el país Mayoritlán no existe, y que las figuras descritas arriba fueron obtenidas de hacer en una computadora una simulación de elección, asignando al azar la preferencia de cada ciudadano, de manera que en promedio la preferencia electoral ronde alrededor del 60%. Repitiendo el ejercicio muchas veces, para muchas realizaciones independientes de esta elección, es decir, para un ensemble electoral, como diríamos los físicos, obtendríamos resultados como los mostrados en la gráfica 3.

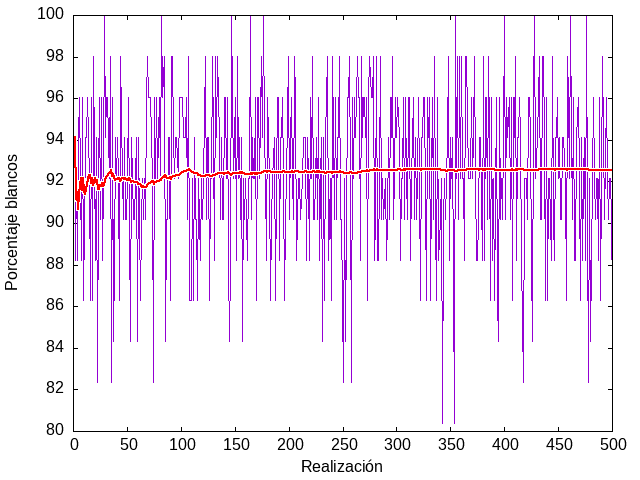
Figura 3: Porcentaje de diputados (línea delgada) del Partido Azul y su promedio (línea gruesa) sobre un conjunto de una hasta quinientas realizaciones de una elección en un país de 51 pueblos con 51 habitantes cada uno

La figura muestra que, al repetir la elección sobre muchos países imaginarios, todos ellos con las mismas preferencias electorales en promedio, 60% a favor de azules y 40% a favor de rojos, el resultado favorece a los azules, otorgándoles entre el 80% y el 100% de los escaños. El promedio sobre muchas elecciones similares rápidamente se estabiliza en un número que ronda un poquito arriba de 92%.

La tiranía

El lector estará de acuerdo que, en este escenario, los simpatizantes del partido azul estarán sobre representados en la cámara de diputados, pues constituyendo apenas el 60% de la población, tendrán más del 92% de las diputaciones, mientras que los simpatizantes del Partido Rojo, estarán sub representados, pues a pesar de ser 40% de la población, tendrán menos del 8% de los lugares. Por lo tanto, el 40% de la población estará sujeto a las decisiones que con una gran mayoría tomará, sin necesidad de discusión, negociación, argumentación e investigación, la mayoría blanca. Esto es lo que se conoce como la tiranía de la mayoría. Es muy probable que Ud. conozca algún país en que las mayorías actúen de dicha forma.

Fluctuaciones

¿A qué se debe este fenómeno? Note que si todos los pueblos fueran idénticos entre sí y por tanto idénticos al pueblo promedio, en cada uno ganaría el diputado azul con 60% de los votos. Afortunadamente, el partido minoritario puede ganar ocasionalmente gracias a las fluctuaciones. El número de votos Vi que obtengan los azules en el i-ésimo pueblo puede diferir de su promedio (30.6, correspondiente al 40% de 51) debido a una fluctuación ΔVi. Suponiendo que cada votante decide por quien votar independientemente de lo que decidan sus vecinos, estas fluctuaciones corresponderían a las de una distribución estadística conocida como binomial (ver la referencia (1)) y su promedio (más bien, la raíz cuadrada del promedio de sus cuadrados) estaría dada por la fórmula ΔV=√(NPQ), donde N es el número de votantes, P=0.6 es la probabilidad de que un ciudadano vote por los azules y Q=0.4 es la probabilidad de que vote por los rojos. En nuestro caso, N=51 y por tanto ΔV=3.5. Esto significa que con mucha frecuencia se encontrarán fluctuaciones de hasta 3 o 4 votos por arriba o abajo del promedio, y con menor frecuencia fluctuaciones un poco mayores, pero muy rara vez se esperarían fluctuaciones mucho mayores. Las fluctuaciones en el porcentaje de votos se obtienen dividiendo entre el número total N de votantes, Δp=7%. Notamos que una fluctuación de este tamaño no alcanzaría para que en algún pueblo dado gane la votación el candidato del partido minoritario; se requieren fluctuaciones más grandes, las cuales son muy improbables. Por eso el mayoriteo absoluto. Puesto que no es factible elegir diputados que sean un poco azules, en tres de cinco partes, y un poco rojos, en las dos partes restantes, el resultado de la elección corresponde a aplicar una función altamente no lineal a las preferencias del electorado, que mapea un continuo de posibles preferencias entre 0% y 100% a uno sólo de dos resultados, o totalmente rojo o totalmente azul.

Tamaño de la elección

El país Mayoritlán descrito arriba es en realidad muy pequeño. Consideremos un ejemplo donde el número de pueblos y el número de votantes en cada uno se multiplique, digamos, por 10. Los resultados correspondientes a las figuras 1 y 2 se convertirían en las figuras 4 y 5.

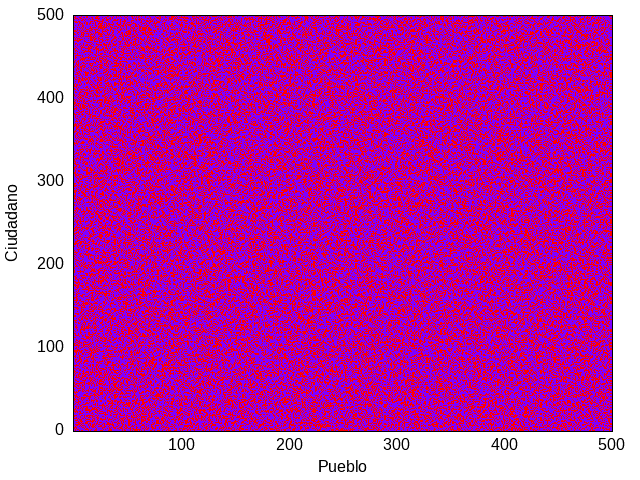
Figura 4: Preferencias electorales como en la figura 1 pero para un país con 500 ciudades y 500 votantes por ciudad.

Viéndola de lejos, la figura 4 se vería como una mancha magenta, un poco más azul que roja. Al reorganizarla como en la figura 5 verificamos que los rojos obtendrían alrededor de 200 votos y los azules alrededor de 300 votos en cada pueblo, con algunas fluctuaciones que podemos calcular como hicimos arriba Δv=√(500×0.6×0.4)=11. Estas fluctuaciones ¡no alcanzarían para que los rojos ganaran en casilla alguna! En este caso, ¡los azules quedarían invictos, ganando el 100% de las diputaciones!

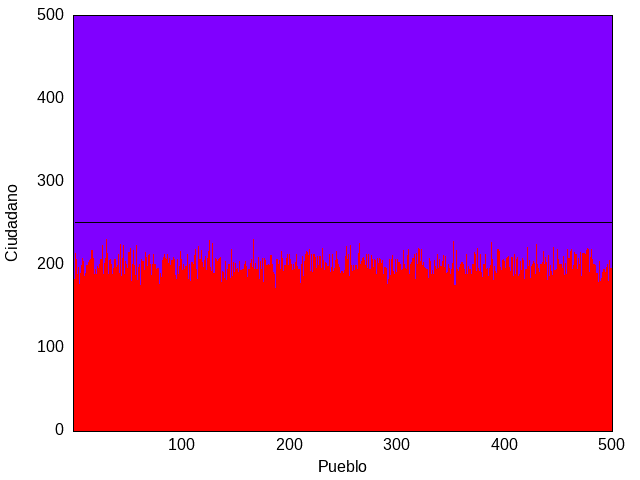
Figura 5: Preferencias electorales como en la figura 2 pero para un país con 500 ciudades y 500 votantes por ciudad.

México

México está dividido en 300 distritos electorales en cada uno de los cuales se elige un diputado en elecciones federales que se llevan a cabo cada 3 años (ver ref. (2)). En junio de 2021 votaron casi 50 millones de ciudadanos, alrededor de 170,000 por cada diputado federal (ver ref. (3)). Suponiendo que la elección hubiese sido entre sólo dos partidos y que el partido mayoritario gozara de una preferencia de alrededor de 60% y el minoritario de alrededor del 40%, como en Mayoritlán, el partido mayoritario hubiese obtenido alrededor de 100 mil votos y el minoritario alrededor de 70 mil. Las fluctuaciones típicas alrededor de estos resultados serían del orden de 200 votos, apenas del 1% del resultado, tan pequeñas que no podrían evitar una gran paliza.

Lecciones

¿Qué podemos aprender del análisis anterior? Por un lado, debe ser claro a los partidos políticos que la competencia les sería sumamente perjudicial de cumplirse los supuestos de nuestro modelo, expuesto arriba, excepto para el partido mayoritario. Quizás el punto más débil del modelo sea la suposición de que cada votante toma su decisión independientemente de la que tomen sus vecinos. Esto es obviamente falso. Los votantes intercambian ideas y puntos de vista con su familia, sus vecinos, sus amigos, sus colegas en el trabajo, los miembros de los equipos deportivos en que participan, de las congregaciones religiosas que frecuentan, los asistentes a sus fiestas, etc. Por tanto, las votaciones están fuertemente correlacionadas geográficamente. Esto hace que las fluctuaciones sean mucho mayores que las que mostramos arriba, y por ello, las elecciones reales son más competidas que lo aquí previsto (ver por ejemplo la ref. (4)). De hecho, es curioso haber observado en elecciones previas que las fluctuaciones en el número de votos recibidos por casilla no sólo fuesen mucho mayores que las aquí descritas, sino que dependan fuertemente del partido. Así, por ejemplo, el número de votos obtenidos por casilla por el PAN ha fluctuado mucho más que el número de votos obtenidos por el PRI, hecho que quizás pueda deberse al efecto de las congregaciones religiosas.

Una lección para los partidos minoritarios es que no les conviene tener un electorado uniformemente distribuido entre toda la población. Es mejor enfocar sus campañas sobre unos cuantos distritos para lograr mayoría en ellos, que hacer crecer uniformemente su preferencia en todo el territorio para finalmente ser mayoriteados en todos lados.

Una lección para los partidos mayoritarios global o localmente, es que en ocasiones les conviene rediseñar los distritos para ganar en un mayor número de ellos, aunque cuando pierdan en otros la pérdida sea estrepitosa. Esto es, por ejemplo, lo que en inglés se conoce como gerrymandering, una práctica de legalidad en muchas ocasiones cuestionable (ver ref. (5)).

Conclusiones

Aunque el modelo desarrollado arriba peca de simplista e implica una sobre representación de las mayorías más alta que la observada en la realidad, es una explicación relativamente simple de qué es y cuál es el origen de este fenómeno, el cual es un problema para todo país que pretenda ser democrático. Es necesario idear e implementar mecanismos para paliarla y para que exista una adecuada representación de toda la población, tanto de las mayorías como de las minorías, en las cámaras legislativas. En México, uno de estos mecanismos es el de los diputados y senadores plurinominales (ver ref. (6)). Bajo éste, hay cierto número de diputados y senadores que se determina a partir del porcentaje total de votos obtenidos en todo el país, no en cada distrito, por los partidos que los postulan. Este mecanismo tiene muchos problemas, como son permitir a los partidos decidir desde antes de la elección, qué candidatos, los que encabecen la lista de postulaciones plurinominales, serían electos casi con certeza, sin que en realidad vote nadie por ellos en particular. Sin embargo, este mecanismo no debe eliminarse (ver ref. (7)) sin simultáneamente proponer una mejor solución al problema de la sobre representación.

Agradecimientos

Este trabajo se realizó con apoyo de DGAPA-UNAM mediante el proyecto IN109822.

Referencias

1. Distribución Binomial, Página del Colegio de Matemáticas, Preparatoria 8, https://bit.ly/3LEUH4b
2. Cámara de Diputados (México), Wikipedia, la enciclopedia libre, https://bit.ly/3ugfIN3
3. Programa de Resultados Electorales Preliminares 2021, Elecciones Federales, INE https://bit.ly/3x3AwZV
4. Luis Mochán, Elecciones presidenciales, México 2006 ¿Anomalías en el PREP y en el CD? Figuras 17-21.
5. Gerrymandering in the United States, Wikipedia https://bit.ly/3DDuY9s
6. Qué son los diputados y senadores plurinominales y cómo se eligen - Grupo Milenio https://bit.ly/3u4qAxh
7. Federico Berrueto, Fin de los plurinominales, SDP Noticias, https://bit.ly/3jllg2x

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos. Desde la Academia de Ciencias de Morelos externamos nuestra preocupación por el vacío que genera la extinción de la Secretaría de Innovación, Ciencia y Tecnología dentro del ecosistema de innovación estatal que se debilita sin la participación del Gobierno del Estado.