Entrelazados

W. Luis Mochán Backal

Instituto de Ciencias Físicas, UNAM

Miembro de la ACMor

mochan@fis.unam.mx

En 2019 fui invitado a participar en una mesa redonda titulada Entrelazamiento cuántico, Alicia en el país de la física y la ficción de lo extraño, como parte de un evento universitario sobre literatura. La mecánica cuántica es una teoría extraña, como extrañas son las aventuras de Alicia en el país de las maravillas, pero muchos de los aspectos raros de la mecánica cuántica se vuelven relativamente comprensibles en el contexto de la física ondulatoria, esa que explica la propagación del sonido, la luz, los sismos y las olas del mar. Sin embargo, hay un aspecto de la mecánica cuántica, el enredamiento cuántico, que es mucho más extraño y que no tiene analogía en la física clásica de las ondas. Entre otras cosas, viola los principios de ser una teoría local y realista. Para ilustrar qué significa ésto, y mostrar la magia del enredamiento y siguiendo el ejemplo de un colega [ver referencia 1] es que elaboré el siguiente diálogo. Debo hacer notar que el tema del diálogo puede parecer banal y poco interesante. Para entender su fondo será necesario para el lector estar muy despierto y atento a detalles aparentemente insignificantes, y probablemente deba tomar una hoja en blanco y un lápiz y hacer algunas cuentas simples.

• ¡No puede ser! ¡Es imposible!
• ¿Qué te pasa Beto?
• Esto es incompatible con cualquier definición razonable de realidad.
• Seguro exageras.
• No Carlos, te lo describiré, pero es todo muy sutil y te tienes que concentrar para entender el asunto que me preocupa.
• Soy todo oídos.
• Tú sabes que soy obsesivo.
• Y compulsivo, diría.
• Y que llevo una bitácora en la que anoto todo, hasta los detalles más irrelevantes.
• No me sorprende.
• Pues Alicia también.
• Siendo tu hermana, es natural que comparta tus obsesiones.
• Ya sabes que en mi familia somos muy poco comunicativos, y desde que se fue del Valle no había hablado con ella, pero ayer le llamé.
• Ya era hora. Y ¿qué cuenta?
• Tristeaba con nostalgia cuando nos dejó y extrañaba la comida del pueblo, hasta que descubrió tres fondas: La Flaca, Don Gordo y Los Huesos.
• ¡Qué casualidad! Así se llaman mis fondas favoritas.
• Y las mías. Curiosamente, las tres tienen sucursales aquí y en la Montaña y sirven los mismos platillos. Resulta que, al igual que yo, Alicia come cada día en una de ellas y todos los días pide una comida corrida.
• ¡Seguro que ella debe tener algo más interesante que contarte!
• Desde luego, pero esta historia se vuelve muy interesante, aunque tendrás que escucharla completa para apreciarlo.
• Bien, continúa.
• Como yo, Alicia escoge al azar a qué fonda ir cada día, tirando un dado. Ayer le tocó comer en Don Gordo y a mí también. El menú era el de siempre y escogimos exactamente los mismos platillos. Al final, por ejemplo, nos ofrecieron café o postre y ambos pedimos café.
• No es una gran coincidencia.
• Por hacer conversación, le pregunté por el día anterior. Anteayer ambos comimos en La Flaca y los dos pedimos postre. Intrigado, saqué mi bitácora y ella la suya. Empezamos a comparar todas nuestras comidas del último año.
• ¡Lo que es no tener qué hacer ni de qué hablar! Y ¿qué hallaron?
• Que nuestra elección de fonda fue efectivamente aleatoria. En el año visitamos alrededor de 120 veces cada una de las tres, sin ningún orden en particular. Terminamos cada comida con café o postre indistintamente, unas 180 veces cada elección, de nuevo, sin orden alguno y sin importar en qué fonda estábamos.
• No es muy sorprendente.
• Claro, aún no llego a lo extraño. Coincidimos en fondas equivalentes en la tercera parte de las ocasiones: En alrededor de cuarenta ocasiones ambos comimos en La Flaca, en otras cuarenta ambos fuimos a Don Gordo y en similar número de días ambos terminamos en Los Huesos.
• Eso es lo esperado estadísticamente, la elección es al azar, el año tiene poco más de trescientos sesenta días y hay nueve posibles parejas de fondas, 360=9 × 40.
• Pero cada una de las veces que coincidió nuestra elección de fonda ¡elegimos los mismos platillos! Por ejemplo, en las más o menos veinte veces en que ambos comimos en Don Gordo y en que, además, ella pidió café, yo también pedí café; en las veinte ocasiones en que ambos comimos en Don Gordo y ella pidió postre, yo también pedí postre. Además, en las veinte ocasiones que ambos fuimos a La Flaca y ella pidió café, yo también pedí café y en las veinte ocasiones…
• Ya, ya, ya entendí. Aquellas veces que eligieron la misma fonda escogieron los mismos platillos. Eso sí es algo raro. Yo hubiera esperado que si ambos son indiferentes ante la elección de fonda y les da igual pedir café que postre, la mitad de las veces en que ella pidió café tú hubieras pedido café y la otra mitad de las veces tú hubieras pedido postre, sin importar en qué fonda estaba cada uno. Pero por otro lado, son hermanos. Quizás haya algo en sus genes o en su educación que los predispone a pedir el mismo platillo cada día. Como si cada mañana se levantaran ambos y recibieran un mensaje común que los incite a ambos bien a tomar café o a tomar postre.
• Todas las mañanas ambos recibimos un pequeño mensaje del Viejo quien rutinariamente nos escribe 'buenos días', pero nada más, y nunca le contestamos. Pero la explicación tiene que ser más complicada, pues no pedimos lo mismo siempre; sólo cuando ambos vamos a la misma fonda, y no sabemos a qué fonda iremos sino hasta el último momento en que tiramos el dado.
• Entonces tendrían que amanecer cada mañana programados de alguna manera, con instrucciones más detalladas del tipo: si vas a La Flaca (F) pedirás café (C), si vas a Don Gordo (G) pedirás postre (P) y si vas a Los Huesos (H) pedirás café (C).
• Eso pensé en un principio. Si de alguna manera yo amanezco con un juego de instrucciones, digamos C, P y C, correspondientes a las fondas F, G y H, y ella amaneciera con las mismas instrucciones CPC, ambos pediríamos lo mismo en caso de ir al mismo changarro, pero podríamos pedir algo distinto para ciertos pares de fonda.
• Lo curioso es que nunca podrías averiguar el juego de instrucciones completo.
• Así es. Sólo averiguaría las instrucciones correspondientes a la fonda a la que sí fui, y a la que fue Alicia, de ser distinta. Nunca podría averiguar la instrucción restante.
• Eso es más curioso entonces. Si cada quien recibe mágicamente un juego de tres instrucciones, pero sólo puede averiguar una, o a lo más, dos de ellas, la restante existe, pero no es observable. Es un bonito problema para un filósofo. ¿En qué sentido existe algo que no es observable?
• Me recuerda al problema de la existencia de los números innombrables, incalculables e indescriptibles. Pero mi hallazgo es más sorprendente. Resulta que a lo largo del año pedimos lo mismo, aproximadamente la mitad de las veces.
• ¿Y eso qué tiene de raro?
• De haber un juego de instrucciones, estarás de acuerdo que cada día tendría que ser uno de los siguientes ocho: CCC, CCP, CPC, CPP, PCC, PCP, PPC, o PPP, y no habría más (ver Figura 1).

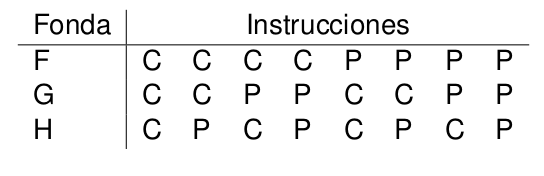
Figura 1. Todos los posibles juegos de instrucciones indicando a cada hermano qué pedir (café (C) o postre (P)) en cada restaurante (La Flaca (F), Don Gordo (G) o Los Huesos (H)).

• De acuerdo.
• Considera por ejemplo que recibiéramos las instrucciones CCP. Ambos coincidiríamos en pedir café en los casos FF, FG, GF, GG y postre en el caso HH, y discreparíamos en los cuatro casos restantes FH, GH, HF y HG. Para los otros juegos de instrucciones pasaría lo mismo, excepto para CCC y PPP para los cuales coincidiríamos para todas las parejas de fondas. Entonces, debimos haber coincidido en cinco o más de cada nueve comidas. Pero sólo lo hicimos en una de cada dos comidas, es decir en cinco de cada diez.
• Caray, la diferencia entre 5/9 y 5/10 no es mucha.
• Pero es significativa.
• Entonces no puede existir un juego alguno de instrucciones. Tu estadística muestra que sus acciones no estuvieron predeterminadas, que ejerciste tu libre albedrío.
• Pero entonces, ¿cómo podríamos explicar entonces los casos en que sí acabamos en la misma fonda? En ellos, nuestra correlación es perfecta. ¿Será que sin darnos cuenta nos comunicamos telepáticamente y nos ponemos de acuerdo? ¿O hay un complot de fondas que nos manipulan como parte de un sofisticado juego perverso?
• Hmmm… Te tengo que contar que hace poco asistí a una charla de física sobre entrelazamiento cuántico. Desde luego, no entendí mucho, pero se me ocurre, ¿no será que, con su mensaje diario de buenos días, tu viejo les manda cada mañana una pareja de partículas enredadas cuánticamente cuyo estado colapsa cuando ordenan la comida y determinan sus elecciones?

¿Qué podemos concluir?

En el diálogo anterior participaron Alicia, su hermano Beto, un amigo Carlos y su padre. Esto es en analogía a todas las descripciones técnicas del fenómeno de enredamiento en la literatura científica, en que explican los fenómenos recurriendo a Alice, Bob y Charlie, pues sus iniciales coinciden con las primeras letras del alfabeto.

Discutir si Alicia o Beto tomaron café o postre puede parecer un tema insignificante para un artículo, pero los hechos aquí narrados violan principios fundamentales como el de la existencia de una realidad local, y esta situación podría realizarse si, como sugiere Carlos al final del diálogo, el padre enviara a cada hijo una de dos partículas entrelazadas cuánticamente como podrían ser dos electrones o dos fotones (referencias [2] y [3]) y midieran alguna de sus propiedades de acuerdo a la fonda que visitan.

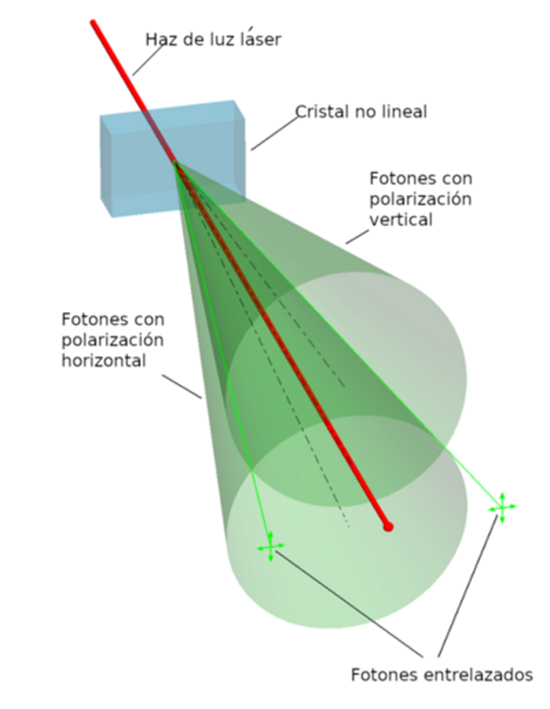
Figura 2. Generación de dos fotones entrelazados. Un fotón linealmente polarizado (cuyo campo eléctrico oscila a lo largo de una línea recta) incide en un cristal no lineal y se parte en dos fotones que se pueden propagar en las direcciones indicadas por la intersección de dos conos. Si se midiera la polarización de uno de ellos y resultara vertical, la del otro también lo haría. Si la del primero resultara horizontal, la del segundo también. Sin embargo, ninguno de los dos tiene una polarización real, bien definida, antes de que se mida o que se mida la de su compañero. (Wikipedia, https://bit.ly/3pdUr2d).

En la Figura 2 se muestra una forma de producir fotones correlacionados. Un sólo fotón cuyo campo eléctrico oscila en una dirección bien definida, con polarización lineal, se parte en dos fotones al atravesar un cristal no lineal. Si se midiera la dirección de oscilación del campo polarización de uno de ellos mediante un polarizador, se vería que como apunta en una dirección, apunta en cualquier otra. La mitad de las veces pasaría y la otra mitad sería absorbido por el polarizador, independientemente de la orientación del mismo. Sin embargo, si un fotón atraviesa un polarizador vertical, el otro atravesaría con certeza otro polarizador vertical. Lo mismo pasaría si ambos polarizadores fueran horizontales o tuvieran cualquier otra dirección coincidente. Es como si la polarización del segundo fotón se definiera al instante en que medimos la polarización del primero.

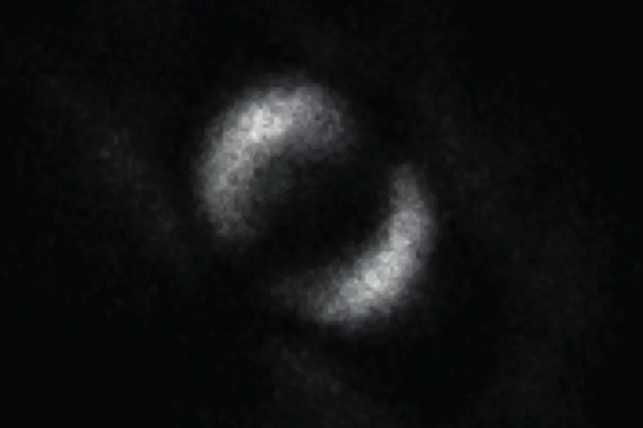
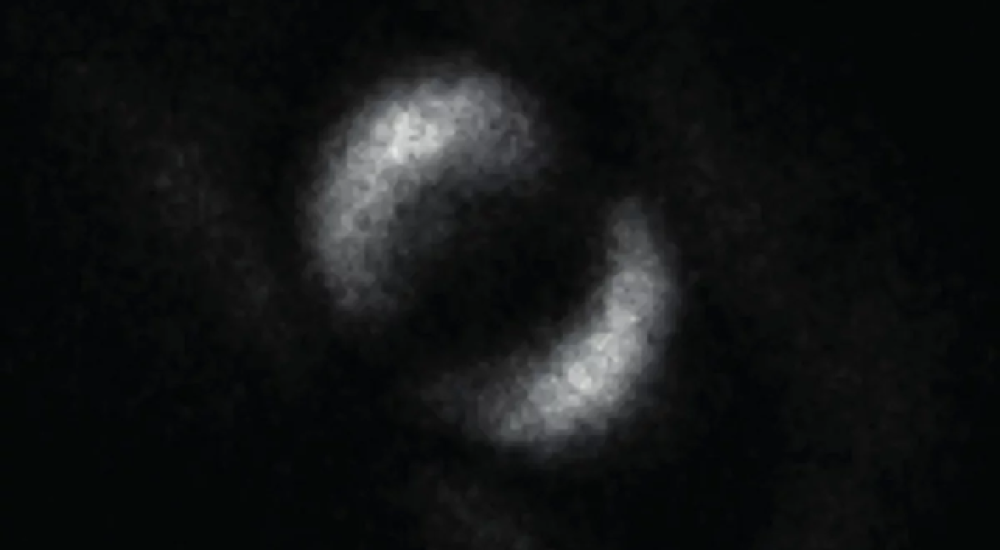
Figura 3: Una de las primeras imágenes de dos fotones entrelazados. https://bit.ly/3pqCUEh

En la Figura 3 mostramos una de las primeras imágenes tomadas de dos fotones entrelazados (ver referencia [4]).

Además de producir correlaciones extrañas entre las decisiones de los dos hermanos, el entrelazamiento o enredamiento cuántico tiene aplicaciones potenciales que revolucionarán nuestra tecnología en el corto y mediano plazo, como el surgimiento de la computación cuántica y su esperada disrupción del encriptamiento tal y como lo conocemos. Hace pocos algunos años celebraba en un congreso el anuncio, con gran bombo y platillo, de que una computadora cuántica de media docena de cubits o bits cuánticos, basados en una molécula de benceno había logrado mostrar que, con una alta probabilidad, 15 podría escribirse como 3×5. Sin embargo, hace menos de dos años Google anunció que su computadora cuántica había finalmente logrado la Supremacía Cuántica (referencia [5]). Más modestamente, pero de manera más inmediata, el enredamiento cuántico se usa hoy en día para encriptar comunicaciones de manera segura y proteger datos sensibles de la vista de ojos curiosos. Por otro lado, el estudio del entrelazamiento cuántico ha impuesto fuertes limitaciones sobre las características que puede tener una teoría física y que, cuándo nos damos el tiempo para ello, nos puede guiar a pensar sobre conceptos tales como el significado de la realidad y la separabilidad de los fenómenos. Desde luego, en este pequeño artículo no pretendí explicar en qué consiste el entrelazamiento cuántico y cómo puede conducir a tantas aplicaciones maravillosas, pero espero haber podido transmitir lo extraño que es el mundo cuántico y las consecuencias que puede alcanzar en nuestra vida cotidiana.

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos. Desde la Academia de Ciencias de Morelos externamos nuestra preocupación por el vacío que genera la extinción de la Secretaría de Innovación, Ciencia y Tecnología dentro del ecosistema de innovación estatal que se debilita sin la participación del Gobierno del Estado.

Referencias

1. Conversación sobre mecánica cuántica. La Unión de Morelos, lunes 20 de junio de 2016. Leyvraz Waltz, François Alain http://www.acmor.org.mx/?q=content/conversaci%C3%B3n-sobre-mec%C3%A1nica-cu%C3%A1ntica-con-un-amigo
2. Is the moon there when nobody looks?, N. D. Mermin, Physics Today, Abril 1985 https://bit.ly/2S418aY.
3. Quantum entanblement, Wikipedia, https://bit.ly/3ielgBU
4. Scientists capture image of quantum entanglement for the first time, Nick Lavars, New Atlas, https://bit.ly/34GAwzv.

La supremacía cuántica ha llegado de la mano de Google y China, pero la computación cuántica aún nos plantea estos desafíos titánicos, Juan Carlos López, Xataka (Enero 2021) https://bit.ly/2SSiZ4R.